9 Autoencoders
This chapter’s HTML notes are in active development. For a more stable version, you can access the PDF notes here.
In previous chapters, we have largely focused on classification and regression problems, where we use supervised learning with training samples that have both features/inputs and corresponding outputs or labels, to learn hypotheses or models that can then be used to predict labels for new data.
In contrast to supervised learning paradigm, we can also have an unsupervised learning setting, where we only have features but no corresponding outputs or labels for our dataset. On natural question aries then: if there are no labels, what are we learning?
One canonical example of unsupervised learning is clustering, which we learned about in Chapter [chap-clustering]. In clustering, the goal is to develop algorithms that can reason about “similarity” among data points’s features, and group the data points into clusters.
Autoencoders are another family of unsupervised learning algorithms, in this case seeking to obtain insights about our data by learning compressed versions of the original data, or, in other words, by finding a good lower-dimensional feature representations of the same data set. Such insights might help us to discover and characterize underlying factors of variation in data, which can aid in scientific discovery; to compress data for efficient storage or communication; or to pre-process our data prior to supervised learning, perhaps to reduce the amount of data that is needed to learn a good classifier or regressor.
9.1 Autoencoder structure
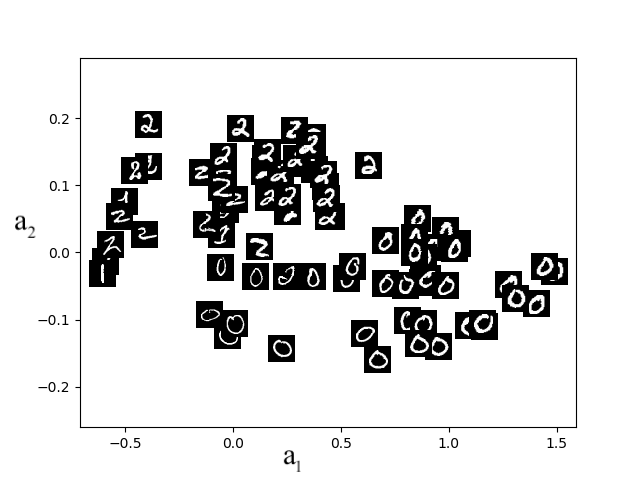
Assume that we have input data \(\mathcal{D} = \{x^{(1)}, \ldots, x^{(n)} \}\), where \(x^{(i)}\in \mathbb{R}^d\). We seek to learn an autoencoder that will output a new dataset \(\mathcal{D}_{out} = \{a^{(1)}, \ldots, a^{(n)}\}\), where \(a^{(i)}\in \mathbb{R}^k\) with \(k < d\). We can think about \(a^{(i)}\) as the new representation of data point \(x^{(i)}\). For example, in Fig. 1.1 we show the learned representations of a dataset of MNIST digits with \(k=2\). We see, after inspecting the individual data points, that unsupervised learning has found a compressed (or latent) representation where images of the same digit are close to each other, potentially greatly aiding subsequent clustering or classification tasks.
Formally, an autoencoder consists of two functions, a vector-valued encoder \(g : \mathbb{R}^d \rightarrow \mathbb{R}^k\) that deterministically maps the data to the representation space \(a \in \mathbb{R}^k\), and a decoder \(h : \mathbb{R}^k \rightarrow \mathbb{R}^d\) that maps the representation space back into the original data space.
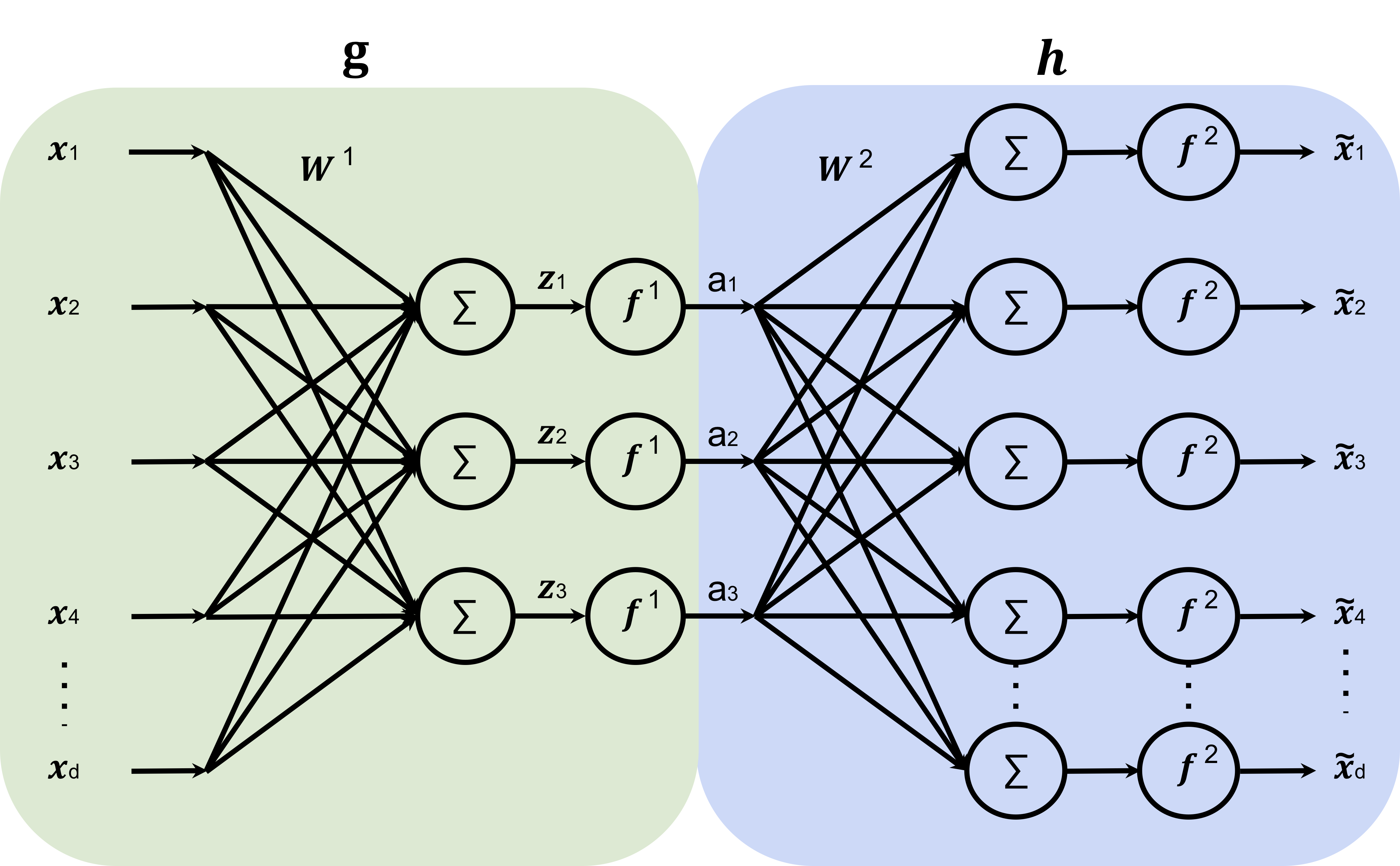
In general, the encoder and decoder functions might be any functions appropriate to the domain. Here, we are particularly interested in neural network embodiments of encoders and decoders. The basic architecture of one such autoencoder, consisting of only a single layer neural network in each of the encoder and decoder, is shown in Figure 1.2; note that bias terms \(W^1_0\) and \(W^2_0\) into the summation nodes exist, but are omitted for clarity in the figure. In this example, the original \(d\)-dimensional input is compressed into \(k=3\) dimensions via the encoder \(g(x; W^1, W^1_0)=f_1(W{^1}^T x + W^1_0)\) with \(W^1 \in \mathbb{R}^{d \times k}\) and \(W^1_0 \in \mathbb{R}^k\), and where the non-linearity \(f_1\) is applied to each dimension of the vector. To recover (an approximation to) the original instance, we then apply the decoder \(h(a; W^2, W^2_0) = f_2(W{^2}^T a + W^2_0)\), where \(f_2\) denotes a different non-linearity (activation function). In general, both the decoder and the encoder could involve multiple layers, as opposed to the single layer shown here. Learning seeks parameters \(W^1, W^1_0\) and \(W^2, W^2_0\) such that the reconstructed instances, \(h(g(x^{(i)}; W^{1}, W^1_0); W^{2}, W^2_0)\), are close to the original input \(x^{(i)}\).
9.2 Autoencoder Learning
We learn the weights in an autoencoder using the same tools that we previously used for supervised learning, namely (stochastic) gradient descent of a multi-layer neural network to minimize a loss function. All that remains is to specify the loss function \(\mathcal{L}(\tilde{x}, x)\), which tells us how to measure the discrepancy between the reconstruction \(\tilde{x} = h(g(x; W^{1}, W^1_0); W^{2}, W^2_0)\) and the original input \(x\). For example, for continuous-valued \(x\) it might make sense to use squared loss, i.e., \(\mathcal{L}_{SE}(\tilde{x}, x) = \sum_{j=1}^{d} (x_j - \tilde{x}_j)^2\). Learning then seeks to optimize the parameters of \(h\) and \(g\) so as to minimize the reconstruction error, measured according to this loss function: \[\min_{W^{1}, W^1_0, W^{2}, W^2_0} \sum_{i=1}^n \mathcal{L}_{SE}\left(h(g(x^{(i)}; W^{1}, W^1_0); W^{2}, W^2_0), x^{(i)}\right)\]
9.3 Evaluating an autoencoder
What makes a good learned representation in an autoencoder? Notice that, without further constraints, it is always possible to perfectly reconstruct the input. For example, we could let \(k=d\) and \(h\) and \(g\) be the identity functions. In this case, we would not obtain any compression of the data.
To learn something useful, we must create a bottleneck by making \(k\) to be smaller (often much smaller) than \(d\). This forces the learning algorithm to seek transformations that describe the original data using as simple a description as possible. Thinking back to the digits dataset, for example, an example of a compressed representation might be the digit label (i.e., 0–9), rotation, and stroke thickness. Of course, there is no guarantee that the learning algorithm will discover precisely this representation. After learning, we can inspect the learned representations, such as by artificially increasing or decreasing one of the dimensions (e.g., \(a_1\)) and seeing how it affects the output \(h(a)\), to try to better understand what it has learned.
As with clustering, autoencoders can be a preliminary step toward building other models, such as a regressor or classifier. For example, once a good encoder has been learned, the decoder might be replaced with another neural network that is then trained with supervised learning (perhaps using a smaller dataset that does include labels).
9.4 Linear encoders and decoders
We close by mentioning that even linear encoders and decoders can be very powerful. In this case, rather than minimizing the above objective with gradient descent, a technique called principal components analysis (PCA) can be used to obtain a closed-form solution to the optimization problem using a singular value decomposition (SVD). Just as a multilayer neural network with nonlinear activations for regression (learned by gradient descent) can be thought of as a nonlinear generalization of a linear regressor (fit by matrix algebraic operations), the neural network based autoencoders discussed above (and learned with gradient descent) can be thought of as a generalization of linear PCA (as solved with matrix algebra by SVD).
9.5 Advanced encoders and decoders
Advanced neural networks that build on the encoder-decoder conceptual decomposition have become increasingly powerful in recent years. One family of applications are generative networks, where new outputs that are “similar to” but different from any existing training sample are desired. In variational autoencoders the compressed representation encompasses information about the probability distribution of training samples, e.g., learning both mean and standard deviation variables in the bottleneck layer or latent representation. Then, new outputs can be generated by random sampling based on the latent representation variables and feeding those samples into the decoder.
Transformer neural networks use multiple encoder and decoder blocks, together with a self-attention mechanism to make predictions about potential next outputs resulting from sequences of inputs. Such transformer networks have many applications in natural language processing and elsewhere. We will learn about sequential models in Chapter [chap-rnn].